K-epsilon models
From CFD-Wiki
Contents |
Introduction
The K-epsilon model is one of the most common turbulence models, although it just doesn't perform well in cases of large adverse pressure gradients (Reference 4). It is a two equation model, that means, it includes two extra transport equations to represent the turbulent properties of the flow. This allows a two equation model to account for history effects like convection and diffusion of turbulent energy.
The first transported variable is turbulent kinetic energy,  . The second transported variable in this case is the turbulent dissipation,
. The second transported variable in this case is the turbulent dissipation,  . It is the variable that determines the scale of the turbulence, whereas the first variable,
. It is the variable that determines the scale of the turbulence, whereas the first variable,  , determines the energy in the turbulence.
, determines the energy in the turbulence.
There are two major formulations of K-epsilon models (see References 2 and 3). That of Launder and Sharma is typically called the "Standard" K-epsilon Model. The original impetus for the K-epsilon model was to improve the mixing-length model, as well as to find an alternative to algebraically prescribing turbulent length scales in moderate to high complexity flows.
As described in Reference 1, the K-epsilon model has been shown to be useful for free-shear layer flows with relatively small pressure gradients. Similarly, for wall-bounded and internal flows, the model gives good results only in cases where mean pressure gradients are small; accuracy has been shown experimentally to be reduced for flows containing large adverse pressure gradients. One might infer then, that the K-epsilon model would be an inappropriate choice for problems such as inlets and compressors.
To calculate boundary conditions for these models see turbulence free-stream boundary conditions.
Usual K-epsilon models
Miscellaneous
References
[1] Bardina, J.E., Huang, P.G., Coakley, T.J. (1997), "Turbulence Modeling Validation, Testing, and Development", NASA Technical Memorandum 110446.
[2] Jones, W. P., and Launder, B. E. (1972), "The Prediction of Laminarization with a Two-Equation Model of Turbulence", International Journal of Heat and Mass Transfer, vol. 15, 1972, pp. 301-314.
[3] Launder, B. E., and Sharma, B. I. (1974), "Application of the Energy Dissipation Model of Turbulence to the Calculation of Flow Near a Spinning Disc", Letters in Heat and Mass Transfer, vol. 1, no. 2, pp. 131-138.
[4] Wilcox, David C (1998). "Turbulence Modeling for CFD". Second edition. Anaheim: DCW Industries, 1998. pp. 174.

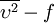 model
model
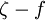 model
model